![]() 問31の解答
問31の解答
<解説>
気付いてしまえば答えの候補はすぐに求められます。
そのために、まずは「列」というものを考えます。
正六角形の巣穴が一直線に並んでいる部分を考えるのですが、……言葉では言い表しにくいので、例をあげます。(^^;
列の例としては、下図のようなものが考えられます。
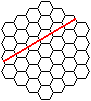
では、一辺に巣穴が4個並んでいるときに、「列」はいくつあるかというと…
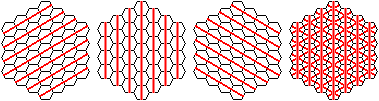
“|”の向きの列を数えてみると7列あります。ということは、“\”や“/”の向きも7列ありますから、合計7×3=21列。
さて、ここで互いに相手のナワバリの中に入っている2匹の蜂を考えてみましょう。例えば次のような状態。
上の図の2匹の蜂のナワバリには、もう1匹も蜂が住むことはできません。
このとき、蜂が住むことが出来ない場所は5列できたことになります。
しかし実は、上の例でなくとも、相手のナワバリの中に入っている2匹の蜂がいれば、その2匹が相手のナワバリに入っている限り必ず蜂が住むことが出来ない場所は5列できるのです!(自分でいろいろと蜂の配置を変えて確かめてみてください)。
裏を返せば、蜂の住んでいない列が5列あれば、うまく配置することにより蜂を新しく2匹住ませることができるだろうと推定できます。…(★)
ということは、(★)より、計算上(1)の21列では、21÷5=4(あまり1)より、蜂は多くても4×2=8匹しか住むことができません。
(計算では1列分あまっていることになりますが、ここで9匹目の蜂を追加するためには3列分のあまりがなければならないことに注意してください。)
さて、この「8匹」というのはあくまで計算上ですから、配置例をあげておきましょう。
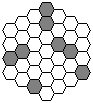
上のような配置例をあげることができたので、(1)の答えは8匹です。
なお、配置例は試行錯誤で探します(配置例はたくさんあるので、このくらいなら試行錯誤でも大丈夫でしょう(^^;;)
相手のナワバリの中に入っている2匹の蜂は隣り合っていると決めつけて考えれば見やすくなるし、作業も多少楽になるでしょう。
(2)も同様に考えます。
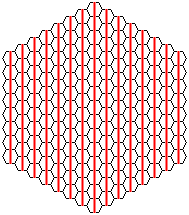
“|”の向きの列を数えてみると15列あります。ということは、“\”や“/”の向きも15列ありますから、合計15×3=45列。
一辺に巣穴が2個並んでいる時は9列、3個並んでいる時は15列、4個並んでいるとき21列…と規則を読んでも求められます。
(★)より、計算上は45÷5=9より、蜂は多くても9×2=18匹しか住むことはできません。
あまりの列もないので、あとは18匹の配置例を探せばいいだけです。
ところが、これだけ巣が大きいと、(1)のように試行錯誤で考える気はとてもじゃないけど起こりませんね(^^;
そこで、次のことに気付けば何とかなります。
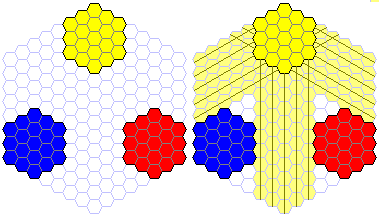
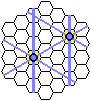
左上の図で青、黄、赤の3つの部分に注目してください。
右上の図より、黄の部分に蜂はどのように配置しようとも、青や赤に住む蜂のナワバリには絶対に入らないことが分かります。
これは青や赤に住む蜂にもいえることです。
このことから、青、黄、赤の各部分に6匹ずつ住ませることができれば、18匹の配置も可能となります。
黄の部分に6匹の配置は、次の図のようにすると可能です。
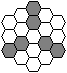
よって、18匹の配置として次のようなものが考えられます。
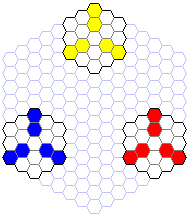
よって、(2)の答えは18匹、です。
…こうやって解説を作っているうちに、「(1)は1辺に3個の方がよかったかなぁ...」と思ってしまいました(--;
(中学生以上向け・発展事項)
上のような考えにより、1辺に巣穴がn個並んでいるときに住むことができる蜂の最大値は、
[6(2n−1)/5]匹 ([A]は、「Aの整数部分」を表す)という推測ができます。
n=1,2,4,そしてkを自然数としたときn=(5×3k-1+1)/2の時は正しいことはわかっていますが、予想が本当に正しいかどうかは未確認です。
| 正解;(1)8匹 (2)18匹 |