![]() 問34の解答
問34の解答
<解説>
一見とてつもなくややこしそうですが、可能性をできるだけ絞り込むと実は計算で求められるようになります。
というわけでまずは、絞り込み作業です。
取り得る数に制限にある箇所を列挙します。
「月」は01月〜12月、「日」は01〜31、「時」は00〜23、「分」「秒」は00〜59
なので、これをまとめると下の表のようになりますね。
ただし、「日」では、月によって日数が違うので、現状ではもっと厄介な制限があります。
| 月 | 日 | 時 | 分 | 秒 |
|---|---|---|---|---|
| 十の位は0〜1 十の位が1なら一の位は0〜2 |
十の位は0〜3 十の位が3なら一の位は0〜1 他、「月」により厄介な制限あり |
十の位は0〜2 十の位が2なら一の位は0〜3 |
十の位は0〜5 | 十の位は0〜5 |
『完全時間』は、月-日-時-分-秒の計10個の欄に、0〜9の10個の数字がすべて表示されていることなのですから、同じ数字が2つ表示されていてはいけないことを確認しておきます。
仮に、「月」の十の位を1のときに『完全時間』となるとしてみます。
このとき「月」の一の位は0〜2が、さらに「時」の十の位も0〜2ですから、0と2の位置はこの2箇所で決定です。
次に、「日」の十の位には0〜3が入りますが、0・1・2が他の場所に決まってしまったので、3しか来れません。
しかし、このとき「日」の一の位は0か1が入るのですが、0と1はもう使えません。
つまり、「月」の十の位を1のときに『完全時間』となり得ない… つまり、『完全時間』となるときの「月」の十の位は0と確定します。
ここまでで、先ほどの表を書きなおしましょう。
0の位置が決まったことで、結構絞り込めましたが、もう少し考えてみます。
| 月 | 日 | 時 | 分 | 秒 |
|---|---|---|---|---|
| 十の位は0 | 十の位は1〜3 十の位が3なら一の位は1 他、「月」により厄介な制限あり |
十の位は1〜2 十の位が2なら一の位は1〜3 |
十の位は1〜5 | 十の位は1〜5 |
次に、「日」の十の位を3としてみましょう。
すると、「日」の一の位は1に決まります。
このとき「時」の十の位は(1が使えないので)2に決まります。
しかし、「時」の十の位が2の時の「時」一の位は1〜3のはずが、1・2・3の位置は既に決まってしまったので不適当です。
つまり、「日」の十の位に来る数は3ではないことがわかりました。
もう1度、表を書きなおします。
| 月 | 日 | 時 | 分 | 秒 |
|---|---|---|---|---|
| 十の位は0 | 十の位は1〜2 月が「02」の時、01〜28 |
十の位は1〜2 十の位が2なら一の位は1〜3 |
十の位は1〜5 | 十の位は1〜5 |
「日」の十の位に3が来れなくなったことで、厄介な制限がだいぶ少なくなりました。
でも、もう少し考えると、「日」の厄介な制限はなくなります。
「日」と「時」の十の位はともに1か2しか来れないのですから、1と2はこの2箇所で確定します。
このとき、「月」は03〜09の7通りのみとなります。(1も2も使えないので、01・02・10・11・12はNG)
これで「月」の02があり得なくなった為、「日」の厄介な条件…月が「02」の時、01〜28…が外せます!
表の確定版はこちらです。
| 月 | 日 | 時 | 分 | 秒 |
|---|---|---|---|---|
| 03〜09 | 十の位は1〜2 | 十の位は1〜2 十の位が2なら一の位は3 |
十の位は3〜5 | 十の位は3〜5 |
いよいよ計算です。
<甲>「日」の十の位が1のとき

「時」の十の位は2です。すると「時」の一の位は3と決まります。
このとき、「分」「秒」の十の位には4か5のいずれかが来ることになります。
これで0〜5の配置が決まったため、「月」「日」「分」「秒」の一の位には6〜9が当てはまります。
(「分」「秒」の十の位のあてはめ)×(「月」「日」「分」「秒」の一の位のあてはめ)
=(2×1)×(4×3×2×1)=48秒
<乙>「日」の十の位が2のとき
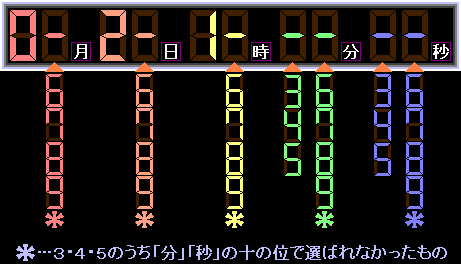
「時」の一の位は1です。
このとき、「分」「秒」の十の位には3・4・5のいずれかが来ることになります。
「月」「日」「時」「分」「秒」の一の位には6〜9か、“3・4・5のうち「分」「秒」の十の位で選ばれなかった数1個”があてはまります。
(「分」「秒」の十の位のあてはめ)×(「月」「日」「時」「分」「秒」の一の位のあてはめ)
=(3×2)×(5×4×3×2×1)=720秒=12分
以上から、48秒+12分=12分48秒が答えとなります。
| 正解;12分48秒 |