問61こたえ

戻る

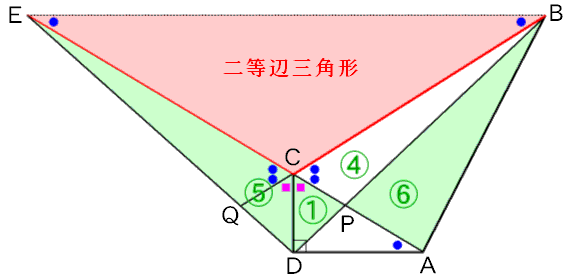
このとき、３点Ｅ・Ｃ・Ａは一直線上に並びます。…(甲)
何故なら、 角ＤＣＡ＝■ とすると、△ＣＤＡが直角三角形であることから ●＋■＝９０度 です。
これより角ＥＣＰ＝●■●■＝９０×２＝１８０度 となることから説明できます。

次に、△ＥＣＢは二等辺三角形です。
これは簡単で、折り返しより ＣＢ＝ＣＥ（＝５０cm） だから。
よって、 角ＣＢＥ＝角ＣＥＢ となります。　…(乙)

ところで、(甲)より角ＡＣＢは、△ＥＣＢの内角Ｃの外角といえます。
三角形の外角の法則から、 角ＡＣＢ＝角ＣＢＥ＋角ＣＥＢ となります。
角ＡＣＢ＝●● と表せたのだから、(乙)より角ＣＢＥ＝角ＣＥＢ＝● ですね。　…(丙)

(丙)より、 ●＝角ＢＥＡ＝角ＣＡＤ が成立します。
これはつまり……そう、ＥＢとＤＡは平行であるということですね！
というわけで、四角形ＥＤＡＢは台形であることがわかりました。　…(丁)

ここで台形の有名な性質より、△ＥＤＰと△ＢＰＡの面積が等しくなります。　…(戊)
△ＣＤＰ＝[１]とすれば、△ＢＰＡ＝[６]ですから△ＥＤＰも[６]です。
（戊の略解：△ＥＤＡと△ＢＤＡは底辺と高さが等しいので面積同じ。それぞれから△ＰＤＡを引けば△ＥＤＰと△ＢＰＡ）

△ＥＣＤ＝[６]−[１]＝[５]。
ＥＣ：ＣＰ＝△ＥＣＤ：△ＣＤＰ＝５：１です。
ＥＣ＝ＢＣ＝５０cmだから、ＣＰ＝５０÷５＝１０cmとなります。これが(１)の答え。

また、△ＣＤＢは△ＥＣＤと線対称ですから、これも[５]。
△ＣＰＤ＝[５]−[１]＝[４]とわかりますから、ＤＰ：ＰＢ＝△ＣＤＰ：△ＣＰＢ＝１：４です。
なので、△ＰＤＡと△ＰＡＢの面積比も１：４とわかり、△ＰＤＡ＝[６]÷４＝[１.５]です。

以上より、四角形ＡＢＣＤ＝[１]＋[４]＋[６]＋[１.５]＝[１２.５]と表せます。
７００÷[１２.５]＝５６cm²が[１]です。
求めたいのは△ＰＤＡ＝[１.５]ですから、５６×１.５＝８４cm²で、これが(２)の答えです。

戻る