問64の解答問64の解答
＜解説＞
長さの「和」の「最小値」ならよく見かけますが、長さの「差」の「最大値」とは…？
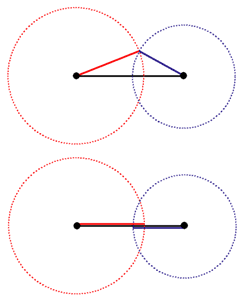線の長さの差に関係する有名な知識として、「三角不等式」があります。
『三角形の一番長い辺の長さは、残りの２辺の長さの和よりは短い』…☆
これは、右図のように、半径の長さがそれぞれ短い２辺である円を描けば理解できます。
さて、☆の不等式を少し言い換えれば、こうなります。
『一番長い辺とそれ以外のうちの一辺の長さの差は、残りの一辺の長さより短い』…★
右下図で、一番長い黒い辺と赤い辺の長さの差は青い辺の長さより短い、ということ。
わかりますか…？(^^;
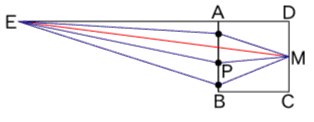しかし、問題図のままで、うまくいきません。
それは、△ＥＰＭで★を使おうとしても「一番長い辺とそれ以外のうちの一辺の長さの差」が一定ではないからです。
（一番長い辺のＥＭが一定値のため、長さの「差」が一定値と比較できない）
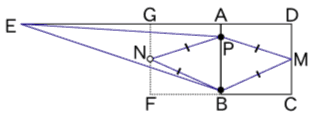そこで、図のように、辺ＡＢについて点Ｍと対称な点をＮとします。
（四角形ＧＦＢＡは、一辺が４２cmの正方形）
すると、Ｐの位置に関わらず、つねにＰＭ＝ＰＮが成立します。
ＥＰとＰＭの長さの差は、ＥＰとＰＮの長さの差と同じということになります。
では、次の図をご覧ください。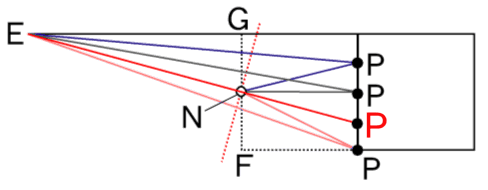
こうすると、ＥＮの長さが一定であることを念頭に。。
ア）３点Ｅ・Ｎ・Ｐが同一直線上にないとき。
３点Ｅ・Ｎ・Ｐを結ぶと三角形ができます。
また、角ＥＮＰは９０度より大きいため（注）、Ｐの位置に関わらず辺ＥＰの長さが最長となります。
△ＥＰＮについて、★より、ＥＰとＰＮの長さの差は、一定値ＥＮの長さよりは短いことが分かります。 …（※）
イ）３点Ｅ・Ｎ・Ｐが同一直線上に並ぶとき。
ＥＰとＰＮの長さの差は、一定値ＥＮと等しくなります。
ア・イより、３点Ｅ・Ｎ・Ｐが同一直線上に並ぶとき、ＥＰとＰＮの長さの差は最大です。
（注）は、直線ＥＮに関して直角に交わる線を引いた時、Ｐはこの線より右側（点Ｅとは異なる側）にあることから、いちおー判断(^^;;
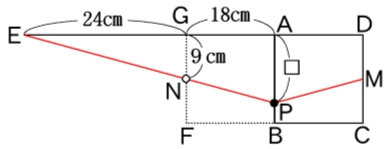
ＥＰとＰＮの長さの差が最大になるとき、△ＥＧＮと△ＥＡＰは相似です。
ＡＰ＝□とすると、ＧＮ＝ＤＭ＝１８÷２＝９cm、ＥＧ＝４２−１８＝２４cmより
２４：９＝４２：□ よって□＝１５.７５(63/4)cmとわかります。
正解；６３／４[１５.７５]cm |