![]() 問68の解答
問68の解答
<解説>
まずは、軽いおもりを用いて実験すると次のようになります。
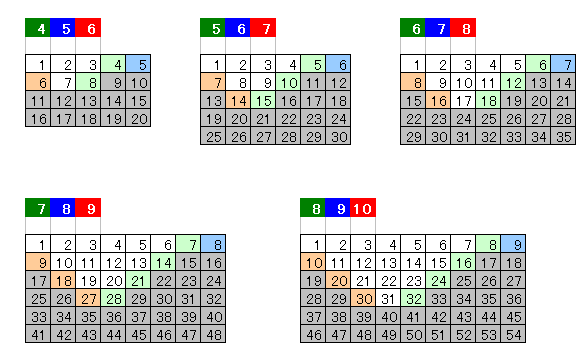
※表の見方
・赤と青と緑…1つのおもりの重さ
・薄赤…赤のおもりのみで作れる重さ
・薄青…青のおもりのみで作れる重さ
・薄緑…緑のおもりのみで作れる重さ
・灰色…複数種類のおもりで作れる重さ
以上のことから、
・白…つりあわせることのできない重さ
となります。
もちろん、つりあわせることのできない重さの砂袋は、重さを特定できない砂袋の有力候補です。
ここで、上の実験から、つりあわせることのできないの個数に規則性を発見します。
緑のおもりの重さが4g(4÷2=2)のとき3+1=4=2×2
緑のおもりの重さが6g(6÷2=3)のとき5+3+1=9=3×3
緑のおもりの重さが8g(8÷2=4)のとき7+5+3+1=16=4×4
…と、緑のおもりの重さが偶数gのとき、つりあわせることのできない重さの個数は四角数(平方数)になっています。
今回は重さを特定できない砂袋が100個未満の場合を求める問題ですね。。
100=10×10ですから、緑のおもりの重さが10×2=20gのとき、つりあわせることのできない砂袋は100個あります。
ところで、つりあわせることのできない重さの砂袋は、重さを特定できない砂袋なのでしょうか?
結論から言うと、それはノーです!
例えば、緑のおもりの重さが4g(青5g、赤6g)のときを考えます。
7gの砂袋は上で検証したとおり、つりあわせることができません。しかし、6gと8gは作ることができます。
ある砂袋を左の皿に置き、6gのおもりを右の皿に置くと左が下がり、8gのおもりを右の皿に置くと右が下がる
この砂袋は6gより重く8gより軽い…砂袋の重さは整数gなのですから、砂袋は7gであると特定できるのです!
同様のことが、緑のおもりの重さが6gのときの17gの砂袋、緑の重さが8gのときの31gの砂袋にも言えます。
同様に考えて、緑のおもりの重さが20gのとき、100−1=99個の砂袋の重さが特定できません。
よって明らかにこの場合に緑のおもりの重さが最大で、このとき青は21g、赤は22gとなります。
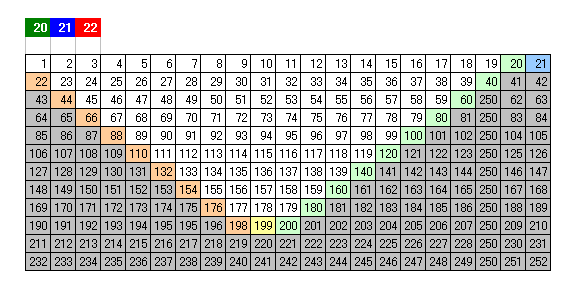
正解;(1)22g (2)179g |