問73の解答問73の解答
＜解説＞
問題の条件から、いかにも「折り返し」「二等辺三角形」がキーポイントになりそうですが…幾つもの山が用意されています。
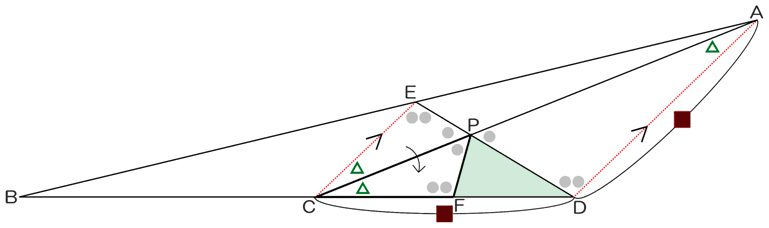
ここで角ＥＣＡ＝▲とすると、(ア)より平行線の錯角で角ＣＡＤも▲。
また、「ＡＤ＝ＣＤ」より△ＡＣＤは二等辺三角形であり、角ＡＣＤも▲。
以上より、角ＥＣＰ＝角ＦＣＰとなり、いよいよ折り返しの芽が出てきました。…(イ)
△ＥＣＰを、ＣＰを折り目として折り返し、移動後の点ＥをＦとすると、(イ)よりＦはＣＤ上にあります。
問題図にあるように、角ＡＰＤ＝●、角ＰＤＡ＝●●と表すことにします。
(ア)より平行線の錯角で角ＰＥＣも●●、折り返したので角ＰＦＣも●●。
また、対頂角より角ＥＰＣ＝●、折り返したので角ＦＰＣも●だから、角ＦＰＥは●●。
以上より、角ＰＦＣ＝角ＦＰＥとなります。…(ウ)
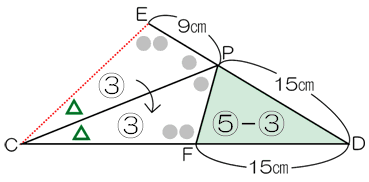そして、△ＰＦＤに注目します。
(ウ)より、角ＰＦＤと角ＦＰＤは(どちらも180−●●と表せるため)等しいことがわかります。
つまり、△ＰＦＤは、ＤＰ＝ＤＦの二等辺三角形ですね！…(エ)
これで答えまでだいぶ近づけました。
ここからは、右図のように△ＥＣＤのみを取り出して考えます。
△ＥＣＰと△ＰＣＤの面積比は、ＥＰ：ＰＤ＝９：１５＝[３]：[５]です。
正解；７５／２[３７.５]cm |