![]() 問51
問51
算数限界編 問51 (2004年4月22日出題 2004年5月22日終了)
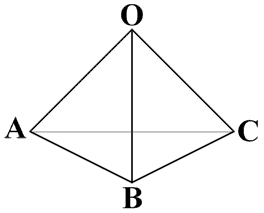
1辺が5cmの正四面体OABCがあります。
この立体を、次のような条件を満たす平面すべてで切断します。
<条件>
・正四面体OABCの切り口の形が正三角形となる
・その切り口の1辺の長さはcmの単位で整数となる
こうして正四面体をバラバラにすると、何種類かの立体に分かれることになります。
このとき、立体の個数が種類別にいくつあるかを、多い順に答えなさい。
1種類だけのときは、その個数のみを答えなさい。
《注意》
すべての切断が終了するまでは、立体は微動すらしません。
切り口はもとの正四面体のいずれかの面と平行であるものとする。
※正解者掲示板に入る際には、以下のルールで入力してください。
例えば立体が3種類でき、立体アが6個、立体イが1個、立体ウが5個できるとすると、(6>5>1より)「6,5,1」と答えます。
| 難易度回答 | 正解者の回答 |
| 無記入 | @@@@@@ |
| 超易問 | |
| 易問 | |
| 普通 | @@ |
| 難問 | @@@ |
| 超難問 | @@@@@@@@ |
正解者一覧(確定)
| 順位 | お名前 | 正解メール到着時刻 |
| 1位 | ひとみん さん | 2004.04/23 00:06:03 |
| 2位 | nobu さん | 2004.04/23 00:44 |
| 3位 | なにわ さん | 2004.04/23 01:11 |
| 4位 | ろろ さん | 2004.04/23 01:21 |
| 5位 | 仮面ランナー サブスリー さん | 2004.04/23 01:37 |
| 6位 | BossF さん | 2004.04/23 04:36 |
| 7位 | 一真 さん | 2004.04/23 07:07 |
| 8位 | 算数ぼけ さん | 2004.04/23 08:13 |
| 9位 | ちず さん | 2004.04/23 17:13 |
| 10位 | tomh さん | 2004.04/23 19:47 |
| 11位 | kasama さん | 2004.04/23 22:58 |
| 12位 | 始 受験勉強君 さん | 2004.04/23 23:53 |
| 13位 | nakakun さん | 2004.04/24 02:34 |
| 14位 | みかん さん | 2004.04/25 22:16 |
| 15位 | 巷の夢 さん | 2004.04/26 07:04 |
| 16位 | 素粒子屋 さん | 2004.04/26 15:43 |
| 17位 | 奥入瀬 さん | 2004.05/16 12:32 |
| 18位 | すてっぷ さん | 2004.05/20 18:25 |
| 19位 | 圭太 さん | 2004.05/22 06:12 |
☆Congratulations!!!☆